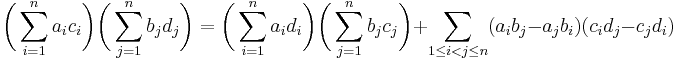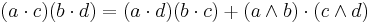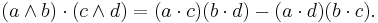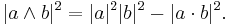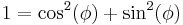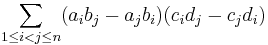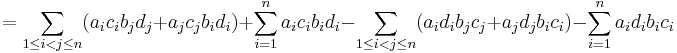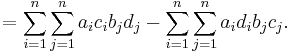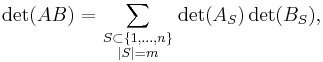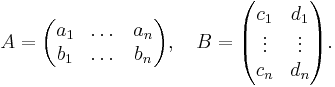Binet–Cauchy identity
In algebra, the Binet–Cauchy identity, named after Jacques Philippe Marie Binet and Augustin-Louis Cauchy, states that [1]
for every choice of real or complex numbers (or more generally, elements of a commutative ring). Setting ai = ci and bi = di, it gives the Lagrange's identity, which is a stronger version of the Cauchy–Schwarz inequality for the Euclidean space 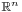 .
.
Contents |
The Binet–Cauchy identity and exterior algebra
When n = 3 the first and second terms on the right hand side become the squared magnitudes of dot and cross products respectively; in n dimensions these become the magnitudes of the dot and wedge products. We may write it
where a, b, c, and d are vectors. It may also be written as a formula giving the dot product of two wedge products, as
In the special case of unit vectors a=c and b=d, the formula yields
When both vectors are unit vectors, we obtain the usual relation
where φ is the angle between the vectors.
Proof
Expanding the last term,
where the second and fourth terms are the same and artificially added to complete the sums as follows:
This completes the proof after factoring out the terms indexed by i.
Generalization
A general form, also known as the Cauchy–Binet formula, states the following: Suppose A is an m×n matrix and B is an n×m matrix. If S is a subset of {1, ..., n} with m elements, we write AS for the m×m matrix whose columns are those columns of A that have indices from S. Similarly, we write BS for the m×m matrix whose rows are those rows of B that have indices from S. Then the determinant of the matrix product of A and B satisfies the identity
where the sum extends over all possible subsets S of {1, ..., n} with m elements.
We get the original identity as special case by setting
In-line notes and references
- ^ Eric W. Weisstein (2003). "Binet-Cauchy identity". CRC concise encyclopedia of mathematics (2nd ed.). CRC Press. p. 228. ISBN 1584883472. http://books.google.com/books?id=8LmCzWQYh_UC&pg=PA228.